El Círculo Unitario
Ángulos en el plano
Ángulos en Posición Estándar
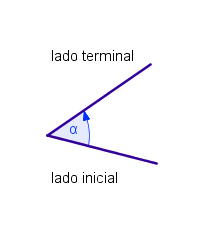
Un ángulo está formado por un lado inicial, un lado terminal y el vértice, como se muestra en la figura:
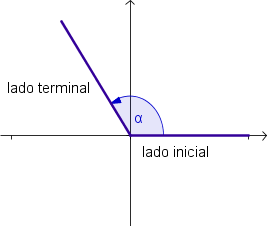
En el sistema de coordenadas cartesianas, se dice que un ángulo está en posición estándar cuando el vértice está en el origen y el lado inicial está en el lado positivo del eje
x.
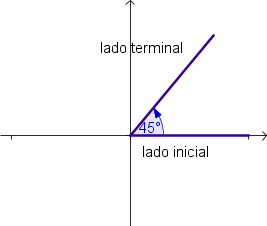
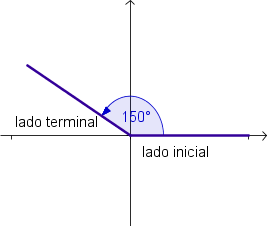
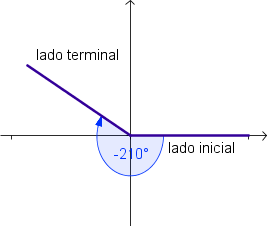
Ejemplos:
Como vemos en los ejemplos de arriba, los ángulos positivos se miden en el sentido contrario a las manecillas del reloj; los ángulos negativos se miden en el sentido de las agujas del reloj.
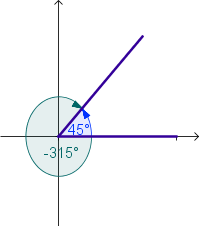
Ángulos Coterminales
Los ángulos que tienen los mismos lados inicial y terminal, se llaman ángulos
coterminales.
Ejemplos:
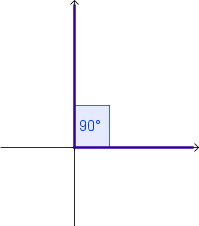
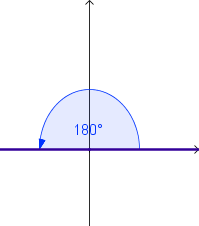
Ángulos Cuadrantales
Los ángulos en posición estándar cuyo lado terminal está en alguno de los ejes coordenados, se llaman ángulos
cuadrantales.
Ejemplos:
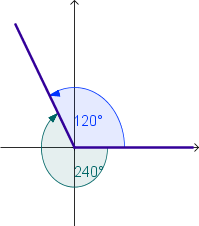
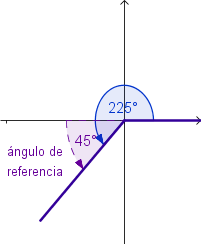
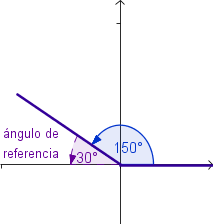
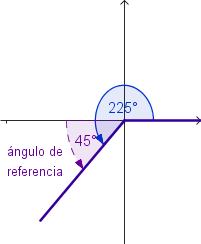
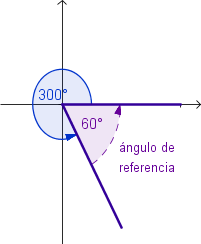
Ángulos de Referencia
El
ángulo de referencia α' de un ángulo α en posición estándar, es el ángulo agudo formado por el lado terminal de α y el eje
x.
Ejemplos:
| El valor absoluto del resultado de una función trigonométrica en cualquier ángulo es igual al resultado de esa función trigonométrica en su ángulo de referencia. Así el valor de una función trigonométrica para un ángulo que mide más de 90° (o menos que 0°) se puede determinar a partir de su ángulo de referencia. Claro hay que utilizar el cuadrante donde el ángulo está ubicado para determinar el signo correcto. |
Periodicidad
Recuerda que podemos definir ángulos que describen más de una vuelta alrededor del círculo. Los valores de las funciones seno y coseno son los mismos para ángulos coterminales, por ejemplo sen(390°) = sen(30°). De esta forma los valores de la función se repetirán periódicamente en forma indefinida.
| Una función es periódica si hay un intervalo positivo de la variable independiente para la cual su gráfica se repite exactamente, o sea una función f es periódica si existe un valor positivo p tal que f (x+p) = f (x) para todo x. El valor p positivo menor tal que f (x+p) = f (x) para todo x se llama el periodo. |
Ejemplos:
| 1. | La gráfica siguiente muestra una función periódica, pues su gráfica se repite cada 180 unidades. Claro se repite cada 360 unidades, cada 540 unidades y cada múltiplo positivo de 180 también. Como 180 unidades es el valor positivo menor para lo cual la gráfica repite, decimos que el periodo es 180.
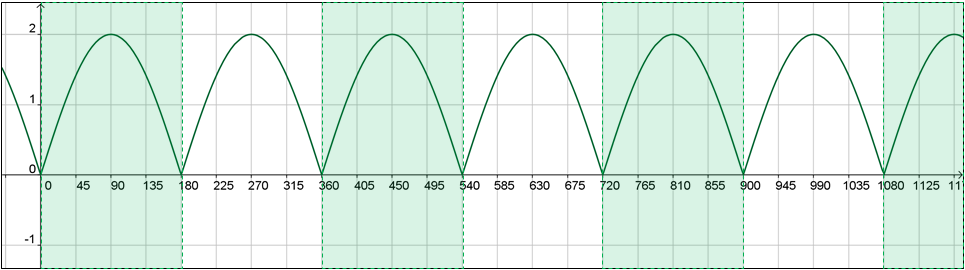 |
| 2. | La función sen(x) es periódica, pues su gráfica se repite cada 360°. En este caso decimos que el periodo es de 360°
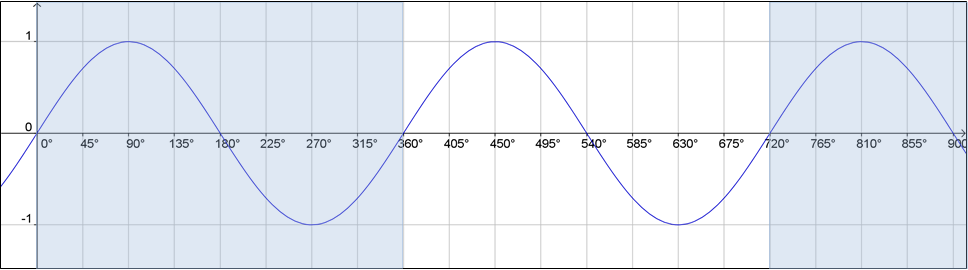 |
| 3. | La función cos(x) es periódica, pues su gráfica se repite cada 360°. Las funciones seno y coseno tiene que ser periódicas porque las coordenadas en el círculo unitario tiene que repetir cada vuelta del círculo es decir cada 360°
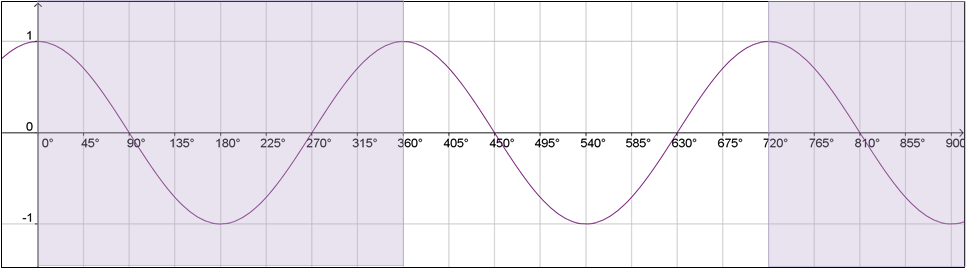 |
Es importante notar que en cada periodo la gráfica es exactamente igual. La siguiente función, por ejemplo,
no es periódica:
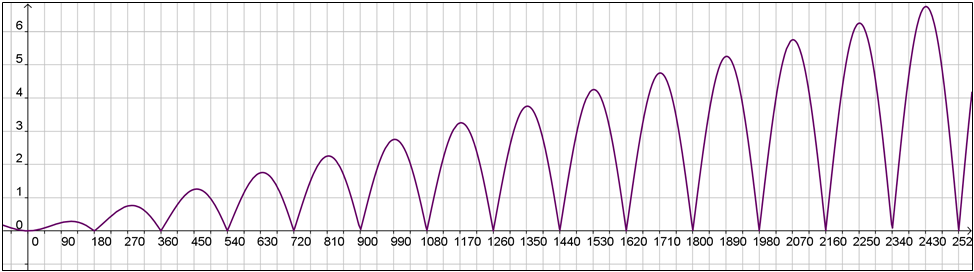
En la siguiente aplicación podemos apreciar la conexión entre la gráfica de la funcion coseno y el punto de intersección del lado terminal del ángulo y el círculo unitiario. Observa que el periodo de la función coseno tiene que corresponder a una vuelta completa del círculo. Cuando se mide en grados el periodo es 360°
Cuando vamos a un parque de diversiones y nos subimos a una estrella, el movimiento de ésta es periódico, pues el movimiento se repite una y otra vez. La siguiente aplicación muestra la gráfica de la altura a la que está una persona que se encuentra en la estrella a través del tiempo.
Created by EDC in Maine staff for the Maine Learning Technology Initiative (MLTI). Adapted from tools by J. Lawlis
Para describir este movimiento periódico matemáticamente necesitamos una función cuyos valores se incrementen, luego disminuyan y repitan el patrón indefinidamente. En una forma similar, en esta lección, vamos a utilizar el círculo unitario para definir las funciones
seno y
coseno. Discutiremos las propiedades de estas funciones y analizaremos sus gráficas.
Para estudiar movimiento y localizaciones en círculos es conveniente fijarnos inicialmente en el círculo mas simple.
El círculo unitario es el círculo de radio 1, centrado en el origen en el plano cartesiano. Su ecuación es:
2 + y 2 = 1
|
Hay muchas maneras de definir localizaciones en el círculo unitario. Vamos a comenzar definiendo una localizacion (
x,
y) en el círculo por el ángulo formado entre (
x,
y) y (0,0) y (0,0) y (1,0).
La localización (0,1) se asocia con 90°
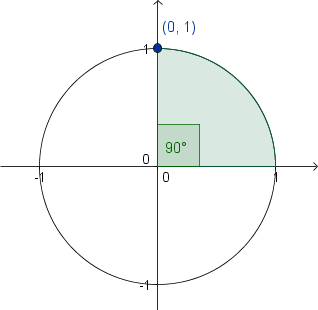 | La localización se asocia con 45°
 |
La localización se asocia con 120°
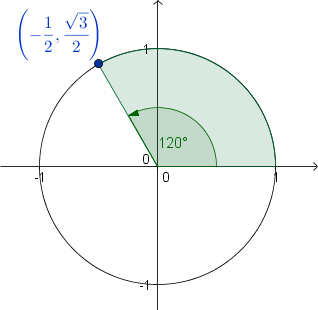 |
La localización (0,-1) se asocia con 270°
|